La geometria che tutti conosciamo, come quella del piano e delle figure geometriche, è nota come Geometria euclidea perché affonda le proprie radici nello studio del matematico greco Euclide. Egli, nel IV-III secolo a.C., ha posto le basi della nostra geometria negli “Elementi”, un’opera mastodontica e ricca di nozioni, in cui partendo da assiomi o postulati e passando attraverso lemmi e proposizioni si arriva alle dimostrazioni di importanti teoremi della geometria, come il teorema di Pitagora.
Tra i cinque postulati all’inizio enunciati, quello che ha destato maggiore interesse è stato fin da subito il V, il quale, secondo la versione di Morris Kline, recita:
“E che se una retta, venendo a cadere su due rette, forma gli angoli interni da una stessa parte minore di due angoli retti, le due rette, prolungate indefinitamente, si incontrano dalla parte in cui sono i due angoli minori di due angoli retti ”.
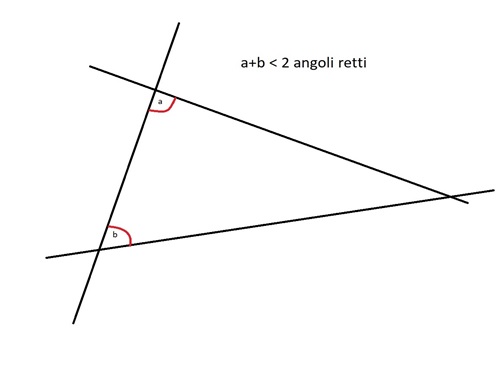
Esso afferma che se una retta taglia altre due rette realizzando dallo stesso lato angoli interni la cui somma è minore di due angoli retti, allora prolungando le due rette esse si incontreranno proprio da quel lato, come nella figura sottostante.
La peculiarità di tale assioma è quella di non mostrare la propria veridicità in modo evidente e molti matematici successivi ad Euclide hanno provato a dimostrare il V postulato a partire dai precedenti, senza riuscirci.
È proprio l’importanza fondazionale che tale postulato assume nella Geometria euclidea che ha spinto alcuni matematici dell’800 ad inventare alcune geometrie alternative, dette non euclidee, in cui viene negato il V postulato di Euclide. Le due più importanti sono la Geometria iperbolica e, soprattutto, quella ellittica o di Riemann.
Nella prima, il V postulato viene sostituito da un assioma in cui si afferma che per un punto esterno a una retta data passa più di una retta parallela (e quindi ne esistono infinite); nella seconda, si asserisce che due rette qualsiasi hanno sempre almeno un punto in comune (ovvero non esistono rette parallele). Una conseguenza immediata di queste modifiche è che se per la Geometria euclidea la somma degli angoli interni di un rettangolo è sempre pari a 180°, per quella iperbolica la somma è inferiore, mentre per quella ellittica è maggiore.
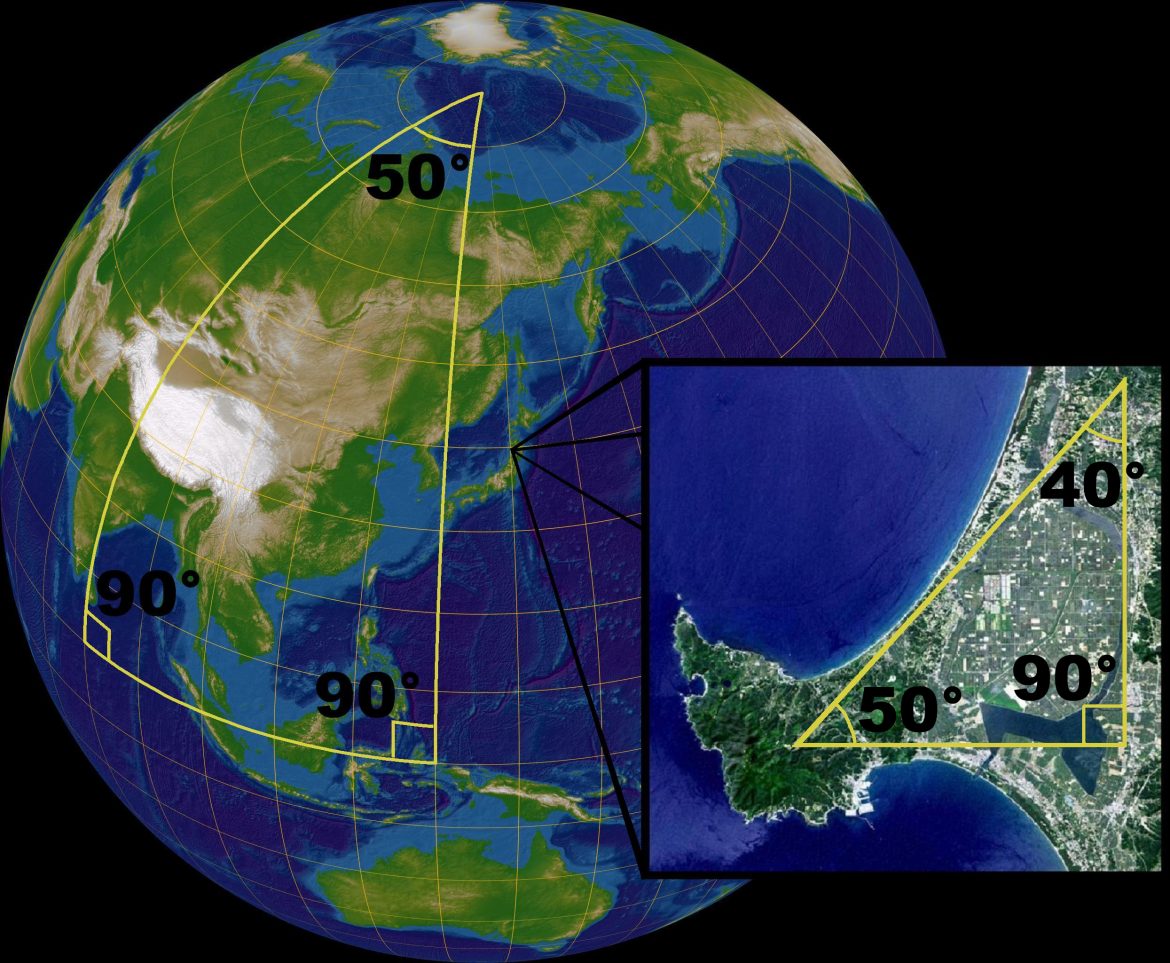
La geometria di Riemann ha assunto un’importanza notevole, perché essa è localmente equivalente alla geometria sferica, ovvero la geometria della superficie di una sfera. Se immaginiamo, infatti, di realizzare un triangolo sulla superficie terrestre seguendo come lati due meridiani e l’equatore (come nella foto di copertina) allora la somma degli angoli interni sarebbe maggiore di 180°. Quindi no, la terra non è piatta, altrimenti la sua geometria sarebbe stata quella euclidea e i triangoli avrebbero avuto come somma degli angoli interni proprio 180°.
Alessandro La Farciola