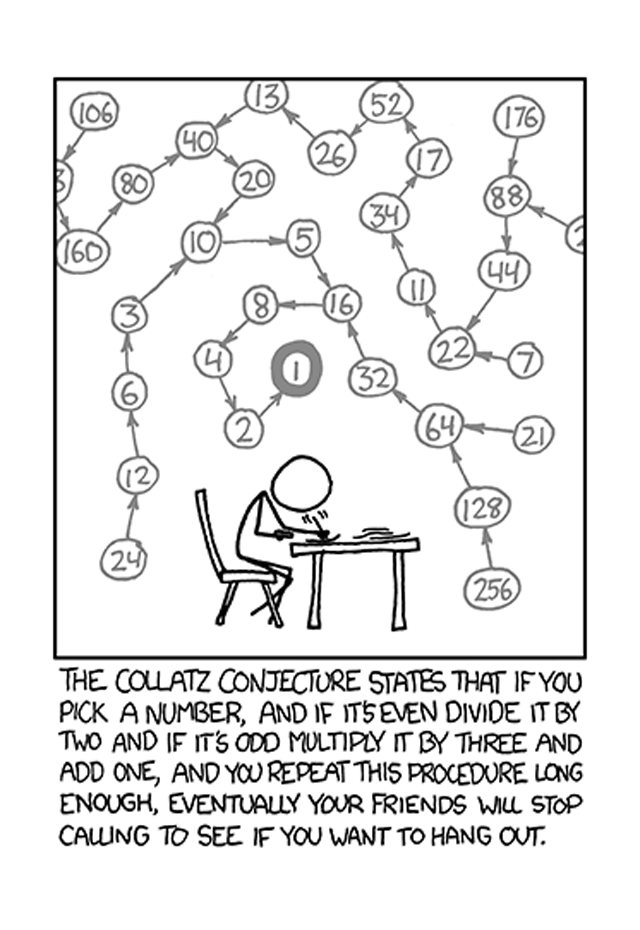

- Si scelga un numero naturale n;
- Se n=1 allora l’algoritmo termina;
- Se n è pari allora si divida per 2, se è dispari si moltiplichi per 3 e si aggiunga 1.
Facciamo alcuni esempi: prendiamo n=10, essendo pari dividiamo per 2 e otteniamo 5, il quale è dispari e quindi bisogna moltiplicare per 3 e aggiungere 1, avendo come risultato 16 da cui 8, 4, 2, 1. Se, invece, n=11 si ottiene la successione 11, 34, 17, 52, 26, 13, 40, 20, 10 e, come prima, 5, 16, 8, 4, 2, 1. La congettura afferma che per qualsiasi scelta del numero di partenza l’algoritmo terminerà, ovvero non si verifica mai un ciclo infinito né la successione diverge all’infinito, ma si raggiungerà in ogni caso 1.
La congettura è vera? Sembrerebbe di sì, basta infatti scegliere a caso il numero di partenza e si ottiene sempre lo stesso risultato (qui si può provare: https://www.mathcelebrity.com/collatz.php?num=+27&pl=Show+Collatz+Conjecture). Anzi, fino ad oggi con l’aiuto dei computer sempre più potenti e veloci si è riuscito ad appurare che per tutti i valori fino a la congettura è verificata. Eppure, non esiste alcuna dimostrazione matematica che ne garantisca la assoluta veridicità.
Con l’evoluzione tecnologica si potranno controllare numeri sempre maggiori, ideando algoritmi ancora più efficienti, ma la comunità scientifica ritiene improbabile che il più piccolo controesempio sia tanto grande. Ciò nonostante, finché non ci sarà una dimostrazione non si potrà essere soddisfatti e la congettura resterà ancora aperta.
Alessandro La Farciola