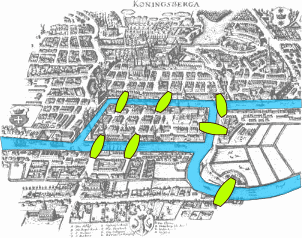
Il problema dei ponti di Kӧnigsberg è uno dei primissimi problemi della teoria dei grafi che nel corso del 1700 è stato discusso formalmente in ambiente matematico. Esso nasce da una situazione concreta di una città reale. Kӧnigsberg, l’attuale Kaliningrad, in Russia, era una città della Prussia orientale percorsa da un importante fiume e alcuni suoi affluenti. Per permettere la comunicazione tra i vari quartieri della città sono stati costruiti sette ponti, come nella figura in alto.
È nato così un interrogativo comune: è possibile con una passeggiata percorrere tutti e sette i ponti attraversandoli una e una sola volta?
Ad una domanda così semplice non corrisponde una soluzione altrettanto semplice. Anche se qualcuno all’epoca provava empiricamente a trovare una risposta, camminando per ore nel centro di Kӧnigsberg, formalmente la soluzione è stata dimostrata da Eulero nel 1741, sfruttando importanti e generali risultati della teoria dei grafi. Il problema, infatti, si può schematizzare come un grafo, ovvero un insieme di nodi che possono essere collegati tra loro attraverso degli archi, diventando come nell’immagine seguente.
In generale Eulero stabilì che:
- Un grafo composto da nodi collegati da un numero pari di archi (nodi di ordine pari) può essere attraversato passando una e una sola volta per tutti i nodi, tornando così al punto di partenza.
- Un grafo che contiene nodi di ordine pari e solo altri due collegati con un numero dispari di archi (nodi di ordine dispari) può essere percorso, ma bisogna partire da uno dei due nodi di ordine dispari e arrivare necessariamente all’altro nodo di ordine dispari.
- Un grafo, infine, che contiene più di due nodi di ordine dispari non può essere percorso interamente senza attraversare archi già toccati in precedenza.
Allora qual è la soluzione del problema originario? Analizzando attentamente il grafo che schematizza la città di Kӧnigsberg con i suoi ponti, si può osservare che esso contiene quattro nodi aventi tutti ordine dispari.
Il problema, quindi, risulta impossibile.
Alessandro La Farciola