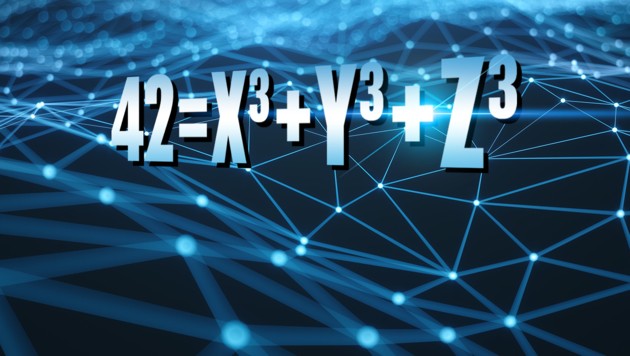
Quali sono i tre numeri che elevati al cubo danno come risultato 42? Può sembrare un rompicapo di facile risoluzione, ma ci sono voluti anni di ricerca e l’utilizzo di un supercomputer per trovarne una soluzione. Il problema è stato formulato a Cambridge nel 1954 e il risultato è stato raggiunto solamente quest’anno. Tutto si riconduce ad una equazione diofantea (che prende il nome da un matematico dell’antica Grecia, Diofanto), ovvero un’equazione in una o più incognite intere (non decimali) di cui si cercano soluzioni intere. La nostra equazione è:
x3 + y3 + z3 = 42
Il quesito originario era quello di risolvere l’equazione: x3 + y3 + z3 = 42 con k che varia da 1 a 100. Gli scienziati avevano trovato la soluzione per ogni valore di k, eccezion fatta per i numeri 33 e 42. Quest’anno, però, il matematico Andrew Booker è riuscito prima a risolvere il problema del 33 e, in seguito, con l’aiuto di uno dei maggiori esperti a livello mondiale di supercomputer e di calcolo parallelo Andrew Sutherland, ha battuto anche il numero 42. In entrambi i casi si è servito di Charity Engine, un “supercomputer planetario”, come loro stessi lo hanno definito, che sfrutta una potenza di circa 500mila pc domestici per arrivare alla risposta giusta. Per k=42 i tre numeri trovati sono x = – 80.538.738.812.075.974; y = 80.435.758.145.817.515 e z = 12.602.123.297.335.631, ovvero numeri dell’ordine di 100 milioni di miliardi, ciascuno con ben 17 cifre.
La sfida però non è ancora conclusa. In matematica, infatti, basta poco per complicare sempre di più un problema: quali sono allora le soluzioni dell’equazione diofantea prima citata per valori di k compresi tra 100 e 1000? Ci sono ancora alcuni vuoti che andrebbero colmati, come ad esempio per i numeri 165, 390, 633, 732, 906.
Alessandro La Farciola