“E … la sfera entra in rete!”. Quante volte abbiamo ascoltato questa frase durante una partita di calcio dalla voce di un telecronista entusiasta che racconta le prodezze di atleti che esaltano folle di tifosi. Ma guardando attentamente un pallone da calcio possiamo davvero affermare che sia esattamente una sfera?
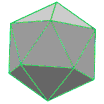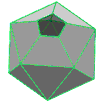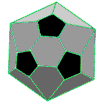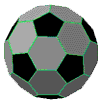
Non proprio. Fabbricare oggetti perfettamente sferici non è per nulla facile. Un pallone da calcio è composto da pentagoni ed esagoni cuciti tra loro: è un solido semiregolare, in particolare un icosaedro troncato. Un solido regolare è un figura tridimensionale che ha per facce poligoni regolari, mentre in uno semiregolare le facce sono costituite da due o più tipi di poligoni regolari. Per un pallone da calcio si parte dall’icosaedro e si procede tagliando i vertici. Si ottiene quindi un modello che ha complessivamente 32 facce: 12 delle quali, pentagonali, sono colorate in nero, e le altre 20 facce esagonali in bianco. In questo modo si ottiene una figura facile da realizzare che approssima abbastanza bene una sfera, soprattutto quando il pallone viene gonfiato e le facce si curvano. Ma perché proprio l’icosaedro? Semplicemente perché è il poliedro regolare che ha il maggior numero di facce.
L’idea di tagliare i vertici di un icosaedro e sostituirli con dei pentagoni era già venuta ad Archimede, uno dei più importanti matematici della storia, il quale nel III secolo a.C. trovò che esistevano soltanto 13 solidi semiregolari, chiamati appunto archimedei.
Probabilmente Messi e Ronaldo riuscirebbero a giocare anche con un icosaedro regolare grazie al loro talento, ma la forma appuntita dovuta ai vertici di certo non aiuterebbe: smussarlo invece lo rende molto più vicino ad un solido sferico, e quindi molto più giocabile.
di Alessandro La Farciola
